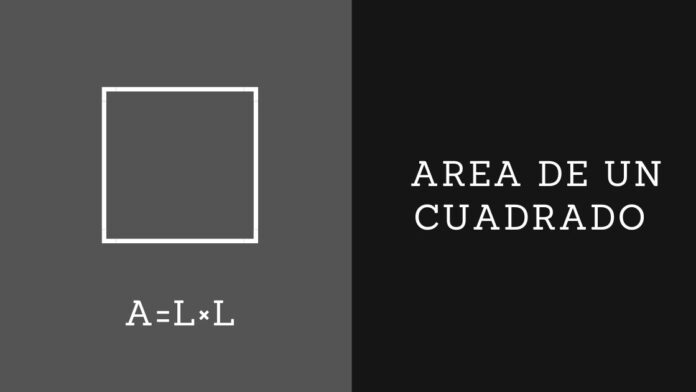
El área de un cuadrado, es un tema común de estudio, ya que suele ser enseñado en la escuela y en la universidad. Por ello, es necesario que comprendas la forma de calcularlo. El cuadrado puede definirse como una figura geométrica plana, que posee cuatro lados iguales y es muy común, siendo una de las figuras más conocidas.
Por esta razón, el área de un cuadrado es la superficie que tiene dicha figura. Esta se conforma de todos de sus lados los cuales encierran toda la superficie. En lo esencial, este posee diferentes medidas y alturas que lo convierten en una figura diferente a las otras. En otras palabras, este posee un área, siendo la que asigna la medida de la superficie. Específicamente debe estar expresada en una unidad de medida, que en este caso son los centímetros. Para lograr encontrar esta área es necesario seguir diferentes fórmulas, que nos permitirán tener el mismo resultado.
Es común pensar que es complicado de resolver, pero no es así.A continuación te enseñaremos la maneras más fáciles para poder calcularlo. Igualmente podrás ver algunos ejercicios, que te ayudarán a entender.
Parte uno para calcular el área de un cuadrado. Primera fórmula
Resulta claro, que para lograr comprender es necesario conocer el significado que tiene cada parte de la fórmula. La primera fórmula expresa una de las maneras más sencillas para poder conseguir el área del cuadrado. Esta se encuentra representada por dos ‘L’, estas significan lados, es decir, los lados que posee el cuadrado.
Por lo tanto usaremos dos cantidades iguales para obtener el resultado deseado. Lo primero que debemos hacer es observar la cantidad de los lados del cuadrado, para comenzar a resolver. Por ejemplo si todos los lados del cuadrado son de 16cm, usaremos esa cantidad para realizar todo el ejercicio.
![\[A=L\times L \]](https://www.solociencias.com/wp-content/ql-cache/quicklatex.com-8d89457ca2495c53c9f0cbd91b5bcde5_l3.png "Rendered by QuickLaTeX.com")
En vez de la “L” colocaremos la cantidad del cuadrado. Al hacerlo solo tendremos que multiplicarla . El resultado de esta operación será el área del cuadrado. Cabe señalar que a la hora de escribir un resultado de un ejercicio, es necesario acompañarlo con la unidad de medida que le corresponde. En estos ejercicios irán acompañados de cualquier unidad de longitud (cm, m, km) al cuadrado.
Segunda fórmula para encontrar en área de un cuadrado
También existe otra forma sencilla que nos permite realizar esta operación. En este caso debes conocer la base y la altura que este tiene. Ahora podemos calcularla usando uno de sus lados con una fórmula diagonal. Por suerte todos sus lados son iguales, lo cual nos permite realizar un proceso menos complicado. Para resolverlo solo tenemos que observar la figura y establecer los datos necesarios, los cuales se sacarán de manera vertical. Seguidamente solo debemos guiarnos de la siguiente fórmula.
![\[A=\ \frac{d^2}{2}\]](https://www.solociencias.com/wp-content/ql-cache/quicklatex.com-ca3abcd02e7c4fe83d97b383bf5ce086_l3.png "Rendered by QuickLaTeX.com")
La letra ‘d’ significa diagonal del cuadrado, que es lo que estaremos usando para realizar el ejercicio. Supongamos que su diagonal es de 10 cm, los cuales debemos colocar para suplantar la letra.
![\[A=d^2\]](https://www.solociencias.com/wp-content/ql-cache/quicklatex.com-80c5bf8cba0894306f827a577cd2e986_l3.png "Rendered by QuickLaTeX.com")
Al momento de colocar la cantidad en la fórmula, solo tenemos que seguirla. Esto demuestra que está elevado al cuadrado, es decir que multiplicaremos dos veces el diagonal, o sea, . Este resultado lo dividiremos con la constante, que en este caso es el número 2.
Cuando dividamos, el resultado obtenido, será el área del cuadrado y terminaríamos el ejercicio.
Tercera fórmula para descubrir el área de cuadrado
Esta última manera nos permite calcular por perímetros (P). En la misma forma, ya entenderemos que los cuadrados cuentan con cuatro lados y tienen el mismo largo. Este perímetro lo usaremos para el cálculo de la superficie (S)
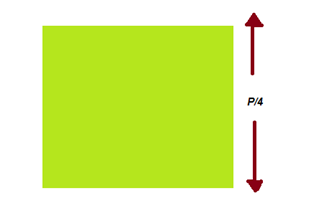
![\[S=\ \frac{P}{4}\]](https://www.solociencias.com/wp-content/ql-cache/quicklatex.com-e03034b9fb8820f8872da242e657cf32_l3.png "Rendered by QuickLaTeX.com")
Para entenderlo, supongamos que nuestro cuadrado tiene un perímetro de 40cm, este número lo posicionamos sobre la ‘P’.Entonces con este resultado dividiremos con el número indicado.
Como vemos, hemos obtenido la superficie del cuadrado, ahora con esta podremos calcular su área. Esto debido a que el área de un cuadrado puede calcularse elevando al cuadrado su superficie.
![\[A=S^2\]](https://www.solociencias.com/wp-content/ql-cache/quicklatex.com-fb3d66727f9aa937552ab7972774f45f_l3.png "Rendered by QuickLaTeX.com")
Ahora lo único que tenemos que hacer, es multiplicar la cantidad obtenida dos veces.
A=100{cm}^2
Ejercicios resueltos de área de un cuadrado.
#1 Ejercicio
Calcular el área cuadrada que posee un lado de 7cm
Solución:
#2 Ejercicio
En un cuadrado que posee cuatro puntos. Existe una línea vertical que conecta un punto con el otro. Este posee 19cm, ahora busca el área de la región cuadrada.
Solución:
#3 Ejercicio
El perímetro de un cuadrado es de 60cm ¿Cuánto medirá cada uno de sus lados?
Solución:
Consejos necesarios para poder realizar ejercicios del área de un cuadrado
Es necesario que leas muy bien el enunciado de cada ejercicio. Porque este será el que te indicará que formula usar para completarlo. En específico si te habla solo de área tendrás que usar la primera. Si te describen una línea diagonal que va desde un punto hacia otro tendrá que implementar la segunda fórmula. Pero si te hablan de un perímetro, tendrás que enfocarte en la última.
Es común, que en varios ejercicios no te muestran un enunciado, sino que te indiquen el cuadrado con los datos que posee. En este caso tendrás que aplicar lo mismo y guiarte en lo que dice cada dato.
Cabe señalar, que a la hora de realizar el ejercicio, lo esencial es guiarte de la fórmula y copiar los resultados de forma ordenada. Esto te permitirá entender el ejercicio de manera más sencilla y no enredarte en el proceso. Asimismo puedes hacerlo por partes o directamente. Si en algún momento te presentan un enunciado el cual no comprendes, lo mejor será realizar el cuadrado con diferentes colores e ir insertando todos los datos. Con esto podrás entenderlo más fácilmente.
