Es una de las figuras geométricas elementales en matemáticas y que muy seguido se suele confundir con la circunferencia.
En el artículo se encuentra el contenido necesario para diferenciar el circulo de la circunferencia, las partes del circulo y la respuesta a la pregunta ¿Es igual el circulo a la circunferencia?
El circulo como figura geométrica
En geometría es una figura básica definida por una región del plano que tiene como borde o limite a una circunferencia. Los puntos que pertenecen al círculo cumplen la siguiente propiedad:
Dado un punto central y un radio, todo punto es parte del circulo si su distancia medida desde el centro es menor que el radio.
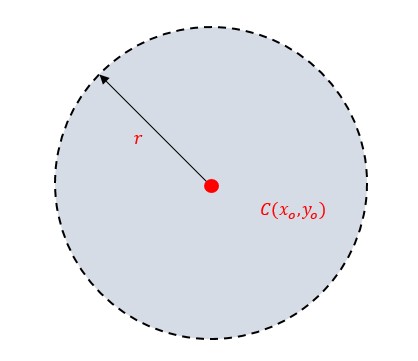
Escrito en forma de ecuación, lo anterior quedaría como:
Sea el centro ![]() y el radio r , todo punto
y el radio r , todo punto ![]() en el círculo cumple la desigualdad:
en el círculo cumple la desigualdad:
![]()
En términos más rigurosos, la región comprendida en dicho intervalo se denomina lugar geométrico del círculo.
Si la circunferencia (perímetro o borde del circulo) se genera al trazar una curva cerrada con el compás, el circulo se formaría al colocar una crayola sobre una hoja, sostener una punta y desplazar a la otra.
Diferencia entre círculo y circunferencia
Es bastante común confundir los términos circulo y circunferencia, incluso utilizarlos como sinónimos para referirse indistintamente a cualquiera de las dos figuras.
- La circunferencia es el borde, es la línea, es el contorno
- El circulo es todo lo que se encuentra dentro, es un área con borde circular
Otro error frecuente es pensar que una figura contiene a la otra. Ni la circunferencia contiene al círculo, ni el círculo está dentro de la circunferencia. Son lugares geométricos totalmente distintos.

Matemáticamente es muy fácil de ver. El lugar geométrico del círculo son todos los puntos con distancia menor al radio respecto al centro. Por otra parte, el lugar geométrico de la circunferencia son todos aquellos puntos cuya distancia respecto del centro es igual al radio.
Lugar geométrico de la circunferencia
![]()
Lugar geométrico del círculo
![]()
Elementos del círculo
Similares a los elementos que se manifiestan en la circunferencia, en el círculo es posible trazar:
- El centro denotado como , es el punto desde el que se miden las distancias
- El radio denotado como , es la distancia que limita el conjunto de puntos dentro del círculo
- El diámetro denotado como , son dos radios trazados de manera colineal en el círculo. Un diámetro es igual a dos radios
- La cuerda denotado como (es una “c” minúscula), segmento de recta que corta al círculo
- El arco denotado como , es una porción del barrido total de un círculo
- La recta tangente denotada como , es la recta que pasa por un solo punto del circulo y es también perpendicular al radio
Fórmula para calcular el área de un círculo
Ya que el círculo delimita una región circular, es decir un área circular, también es posible calcular su superficie. Esta ecuación, junto al resto de fórmulas para el área de figuras elementales, fue de los primeros logros de la geometría elemental.
Dado el radio r, el área del circulo puede ser determinada según la ecuación:
![]()
Si en lugar del radio se tiene el diámetro, la ecuación quedaría como:
![]()
Porciones de un círculo
Son las superficies limitadas por un arco y una o más rectas internas al círculo.
Sector circular. Es una porción de arco delimitada entre dos radios trazados dentro del círculo.

Segmento circular. Es la porción de círculo delimitada por el arco y una cuerda.

Semicírculo. Es la región formada por medio arco de círculo y el diámetro. El diámetro sería una cuerda cuya magnitud es igual a dos veces el radio.